Buckminster Fuller’s Ultra-Micro Computer
Published on 12 July 2014, Fuller’s 119th birthday.
See also: Buckminster Fuller and the Twelfth of July.
“Never show half-finished work.” So said R. Buckminster Fuller in the March 1960 issue of Architectural Design. By the time the phrase “never show half-finished work” appeared in his book Critical Path (1981), “Universal Requirements Checklist” had been renamed “Comprehensively Anticipatory Design Science’s Universal Requirements for Realizing Omnihumanity Advantaging Local Environmental Controls, Which are Omniconsiderate of Both Cosmic Evolution Potentials and Terrestrial Ecological Integrities.”
The evolution of the simple “Universal Requirements Checklist” to “Comprehensively Anticipatory Design Science’s Universal Requirements… ” is representative of Fuller’s process. Fuller’s ideas grow more complex each time they are presented, sometimes obscuring the original idea. But if you can find your way to that central early idea, there is often something of great value.
Everything is equally connected to everything in Fuller’s writing. Fuller was unable to speak of mathematics, ethics, his individual life, global distribution of goods and services - everything - without speaking of all of it. You’d recognize it as the way crazy men talked, if crazy men were courted by publishers and universities all over the planet, and if crazy men earned dozens of ground-breaking patents, and most of all if crazy men and their crazy ideas didn’t turn out to be merely decades ahead of their time. I have some half-finished work by Fuller in which he clearly states an idea decades ahead of when he said it. I also have the finished work, still ahead of its time but nearly impenetrable in how it is presented.
The clearly stated work is a transcription of a recording Fuller made in the late 1960s. The transcriptions reside in Box 9, Folder 3 of the Stanford University Special Collection of R. Buckminster Fuller. The transcriptions document a series of discussions between Fuller and his patent attorney, D. Verner Smythe. The patent was not pursued and does not appear in Inventions, Fuller’s book of patents. The subject of the patent does, however, appear in Fuller’s magnum opus, Synergetics (1975 and 1979). To understand a node of Fuller’s thought requires tracing an idea across many other nodes of Fuller’s thought. But by tracing a line from diary entries through transcribed monologues through published books, Fuller is shown to predict atomic-scale computers nearly forty years before today’s discussion of graphine semi-conductor computers.
The nucleus of Fuller’s story is a simple diary entry from 1 February 1928: “after much philosophical thought while walking about worked out theory of spheres.” By 1939, in a letter intended for publication to Joe Bryant, the walking about had been expanded upon. Now there were thoughts of suicide and murder, a mugging that broke Fuller’s cheek bone (never otherwise confirmed), and a disembodied voice that told him: “You think truthfully. From now on, you need never await temporal attestation to your thoughts.” By the 1970s the story included Fuller floating in the air, surrounded by a sphere of light. Fuller’s story pulses, from an amateur consideration of geometry to a blessing from the hand of God and back again.
Fuller’s theory of spheres is a synthesis of established mathematics, personal insights and numerology. His theory of spheres is a thought experiment that can be reproduced with physical models. Imagine a single sphere floating in space. Add another to it, and a third so that all three are touching each other. Add another sphere that touch only the first two so that the center of each sphere is on a plane. Add a fifth and a sixth sphere, both touching the initial sphere and its neighbor, and the result is six spheres around one. Three more spheres can be nested in the six spaces above and below the plane such that they touch the initial sphere and two of their neighbors.

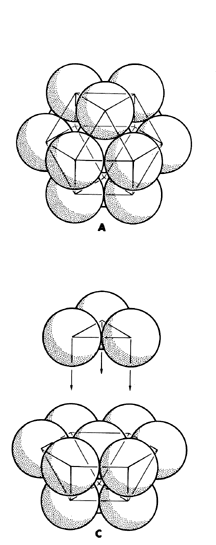
illustrations Copyright (c) 1975 the Estate of Buckminster Fuller.
IF three spheres nested below are staggered so that they alternately nest above and below the plane, the center of every sphere is an equal distance from all of its nearest neighbors, all spheres are an equal distance from the central sphere, and lines drawn from the center of all external spheres to their external neighbor form a cuboctahedron. A cuboctahedron is a polyhedron made up of eight triangular faces and six square faces. It can also be viewed as four interlocking hexagons, or a faceted globe with triangular poles and a hexagon equator.
Sphere-packing is an idea as old as the first stack of cannonballs or oranges. But Fuller’s theory of spheres led to a discovery that is unique. A tetrahedron made with ridged struts and flexible joints will hold its shape even when pressure is applied to a strut or a joint. Most other similarly constructed polyhedron will collapse under pressure. The cuboctahedron will also collapse, but in an interesting way. If pressure is applied to opposing triangular sets of struts, the hexagon between them will ripple. The struts double and form an octahedron (eight triangular faces). Between the cuboctahedron and octahedron, an implied icosahedron polyhedra (twenty sides) can be seen. And with a little hand work, the octahedron can be twisted into a triple-strutted tetrahedron. Fuller called this the “jitterbug transformation” and it is a mathematical insight that is his alone.
Having discovered the jitterbug transformation, Fuller considered it signficant and needed to find a use for it. He made a cuboctahedron cage of curved wire and rotated it on a globe until the wire least overlapped land masses. The cuboctahedron was the basis of his first Dymaxion Projection Map. The cuboctahedron was also the basis for Fuller’s earlier geodesic domes. In Fuller’s earlier geodesic domes a cuboctahedron was puffed up into a sphere, with the triangular and square faces faceted into smaller triangles and squares. Some of the lines that make up the faces run nearly all the way around such a sphere, and these Fuller called great circuits. The great circuits are the struts on Fuller’s earlier geodesic domes. Later he switched to “type two geodesic domes” based on the icosohedra, and an icosohedron based Dymaxion Projection Map. But he never abandoned his attraction to the cuboctahedron. He used it as a symbol for his mail order business in Philadelpha in the early 1980s.
Sphere packing (or as Fuller called it, the closest packing of spheres) twelve around one creates an implied cuboctahedron. If more spheres are placed around cuboctahedron, a larger cuboctahedron is formed. Every new layer of spheres makes a more sharply angled cuboctahedron, never a sphere. With one sphere in the center, the first layer has 12 spheres. The second layer will hold 42 spheres, the third layer 92, the fourth layer 162 and the fifth layer 252. All of these layers and every layer following ends in the number two. Round the number of spheres in a layer (10, 40, 90, 160, 250) and divide the numbers by ten and a progression by the second power is revealed (1, 4, 9, 16, 25). This is also an original discovery by Fuller.
The discovery could not be left as it was found. Fuller’s style of closest packing of spheres could not just be, it had to be meaningful. Adding the number of spheres in the first, second and third layer of spheres around a nucleus sphere (12 + 42 + 92) yields 146 spheres. This is the number of neutrons in the element uranium. Add 92 to 146 to yield 238, the number of neutrons and protons in the element uranium. From this numerological correspondence Fuller concluded that his style of sphere packing was descriptive of the structure of atoms, and thus all matter.
The cuboctahedron as a model for all matter, even this was not inclusive enough for Fuller. He imagined ideas were spheres. Not that spheres are a model for ideas, but that ideas were physical spheres. Some ideas are too specific to be of importance and some ideas are too general to be of importance. Ideas that are too specific are small spheres and ideas that are too general are large spheres. Small idea spheres will cluster around a center, large idea spheres will be pushed further from a central point. One idea is a free-floating nothing, two connected ideas might suggest something worth pursuing, three connected ideas point to a pattern, and four connected ideas form a tetrahedron. A tetrahedron of ideas will include ideas relevant to each thought and exclude irrelevant ideas, because a tetrahedron is the most simple polyhedron that has an inside and an outside (after spheres, I might add). Thus it takes four ideas to make a thought, and the shape of a thought is thus a tetrahedron. Fuller’s theory of spheres was a description of all matter and all consciousness.
These are examples of how Fuller’s thoughts breathed in and out, pulsed and jumped, danced a jitterbug. There was no clear demarkation line between established mathematics, numerology, personal biography, original insights, physical models and cosmic truths. There are good reasons to try and tease out what was original to Fuller and what he took from others, what is actionable and what is ornamentation. One of those good reasons is to speak plainly of when Fuller was decades ahead of his time, because sometimes Fuller was his own worst promoter.
In 1968 and 1969 Fuller met with his attourney Dale D. Klaus. The meeting was a monologue in which Fuller initiated a patent tentatively titled “Energy Systems for Computer Memory.” The trancribed meeting was combined with pages from the 1955 manuscript of what would later be published as Synergetics and Synergetics II. Fuller said his new kind of computer memory would differ from all existing computer memory:
Instead of having linear arrangements which is the way they tend to do things - linear and matrix array, I could do it omnidirectional phenomenon.
Fuller’s computer is a layered cuboctahedrons, each layer made of spheres. Fuller describes the spheres as glass coated with gold, silver, copper or aluminum depending on their location in the array. But Fuller also speaks of individual atoms of these materials, predicting by decades the nanocomputers under development today.
These layers of cuboctahedrons would have arrays of hexagons on their equators, and the nanocomputers of today are made of layers of hexagons. The fifth layer of a layered cuboctahedron of spheres would have the potential for a new nucleus sphere.
Conventional ciruits are described by Fuller as computing in a flat, ninety-degree, x/y array. Fulller’s computer would function in three dimensions at both sixty-degree and ninety-degree angles. The Fuller computer would begin a process with an electric impulse to the central, nucleus sphere. That signal would radiate out in all directions to the surrounding spheres. The radiating signal would terminate based on the strength of the signal, the material of the surrounding spheres, and the distance of a sphere from the nucleus sphere. The pattern of where the signal terminated constitutes stored information. Fuller speaks of his computer as made up of coated glass spheres, but also as single atoms of different elements.
I can lead a wire into one of the spheres at the center of the system and give that a load - and it would have to go out through it’s 12 contact points and by the frequency I give it I am sure I could round a special layer. […] I am planning to have a conductor to the center of the mass of atoms. There would be one atom that makes contact, we wouldn’t even have to see it. Well, the balls, the atoms by the time we get thorugh all the electrons actually have the same… we find with the electron microscope they look just like the same spheres. So by giving the right frequency and going out the right radial distance from there and pick up that information from millions and millions out there at that particular layer.
Three great circles could be done in gold, the four great circles could have been done in silver, the six great circles could have been done in copper and the twelve great circles could be done in aluminum. Now they are all conducting but they are all quite different.
Now about layers. If I were making this myself, say in ping-pong ball size, I couldn’t have very many layers. I figure in this room here I could have 100 layers or so. But if I were to use it… once I made this model then we would know this is exactly the same model as the closest packed spheres, as atoms. So then I would be able to assume millions of layers around a given atom.
Not all atoms but most atoms are packed that way […] So now we would be able for a given frequency… we would know how many special case informations we have stored there and how many relationships there are. […] There is no absolute continuum anyway so even those gold atoms… they happen to be closest and they will simply go from one to the other. But their resistances come in here, too. You will find there is a jump, there is a little jump from atom to atoms. A quantum jump.
There is a resistance difference due to the vertexes they go through. There is a resistance differential. Information can be stored in layer after layer and I think this is a storage system if you talk about compactness, there is nothing to compare it to.
I have re-arranged some of the above quotes to join like ideas, but I have not otherwise edited what Fuller said. His thinking-out-loud is not made up of complete and actionable ideas, but it does clearly point to an atom-sized hex-based system of computer memory. This is identical to the graphine memory systems now under development.
Compare the above rough take on Fuller’s computer with the following description as found in Synergetics:
I am confident that I have discovered and developed the conceptual insights governing the complete family of variables involved in realization by humanity of usable access to the ultimate computer… ultimate meaning here: the most comprehensive, incisive and swiftest possible information-storing, retrieving, and variably processing facility with the least possible physical involvement and the least possible investment of human initiative and cosmic energization. […] We have here the disclosure of a new phase of geometry employing the invisible circuitry of nature. The computer based on such a design could be no bigger than the subvisibly dimensioned domain of a pinhead’s glitter, with closures and pulsations which interconnect at the vector equilibrium stage and disconnect at the icosahedron stage in Milky-Way-like remoteness from one another of individual energy stars. […] The atomically furnished isotropic vector matrix can be described as an omnidirectional matrix of “lights,” as the four-dimensional counterpart of the two-dimensional light-bulb-matrix of the Broadway-and-Forty-second Street, New York City billboards with their fields of powerful little light bulbs at each vertex which are controlled remotely off-and-on in intensity as well as in color. Our four-dimensional, isotropic vector matrix will display all the atom “stars” concentrically matrixed around each isotropic vector equilibrium’s nuclear vertex. By “lighting” the atoms of which they consist, humans’ innermost guts could be illustrated and illuminated. Automatically turning on all the right lights at the right time, atomically constituted, center-of-being light, “you,” with all its organically arranged “body” of lights omnisurrounding “you,” could move through space in a multidimensional way just by synchronously activating the same number of lights in the same you-surrounding pattern, with all the four-dimensional optical effect (as with two-dimensional, planar movies), by successively activating each of the lights from one isotropic vector vertex to the next, with small, local “movement” variations of “you” accomplished by special local matrix sequence programmings. We could progressively and discretely activate each of the atoms of such a four-dimensional isotropic vector matrix to become “lights,” and could move a multidimensional control “form” through the isotropic multidimensional circuitry activating field. The control form could be a “sphere,” a “vector equilibrium,” or any other system including complex you-and-me, et al. This multidimensional scanning group of points can be programmed multidimensionally on a computer in such a manner that a concentric spherical cluster of four-dimensional “light” points can be progressively “turned on” to comprise a “substance” which seemingly moves from here to there. […] The ultra micro computer (UMC) employs step-up, step-down, transforming visible controls between the invisible circuitry of the atomic computer complex pinhead- size programmer and the popular outdoor, high-inthe-sky, “billboard” size, human readability.
The above quotes are from “Nuclear Computer Design,” section 427.00 of Synergetics. This is the same section in which Fuller suggest in antiquity humans were scanned atom by atom at a distant location and teleported to Earth by radio frequencies.
Teleportation aside, compare Fuller’s description of hexagon-based layered computer systems described in 1968 with these recent press releases…
- Multi-layer 3D graphene transistor breakthrough may replace silicon.
- New form of graphene allows electrons to behave like photons.
- All-graphene computer chip could steer us past the 22nm copper and silicon bottleneck.
- IBM builds graphene chip that’s 10,000 times faster, using standard CMOS processes.
It would sound like so much crazy talk, were he not also talking (in a byzantine way) of technologies the world is discovering to be true decades after Fuller described them.
SOURCES (Chronological)
Fuller, R. Buckminster: “Unviersal Requirements Check List.” Architectural Design March 1960.
Fuller, R. Buckminster: “Energy Systems for Computer Memory.” Unpublished manuscript 1968-1969.
Fuller, R. Buckminster: Synergetics. Macmillan Publishing Co. 1975.
Fuller, R. Buckminster: Synergetics II. Macmillan Publishing Co. 1979.
Fuller, R. Buckminster: Critical Path. New York: St. Martin’s Press 1981.
Lorance, Loretta: Becoming Bucky Fuller. Cambridge: MIT Press 2009.
Trevor Blake is the the author of The Buckminster Fuller Bibliography and The Lost Inventions of Buckminster Fuller.