Buckminster Fuller Bibliography
Buckminster Fuller Bibliography by Trevor Blake.
One thousand five hundred entries by and about Buckminster Fuller. Books, magazines, newspapers and ephemera published between 1914 and 2015.
Richard Buckminster “Bucky” Fuller (1895 – 1983) was a public speaker, author, mathematician and inventor. Fuller is best known as the popularizer of geodesic domes in architecture. He attempted to apply the most recent discoveries of science to the most basic of human needs such as shelter and transportation, without regard for precedent or profit or power, doing more with less. He called this process design science.
Paperback
260 pages
Introduction, Bibliography, Index
$17.50
ISBN 978-1944651022
Buckminster Fuller’s Ultra-Micro Computer
Published on 12 July 2014, Fuller’s 119th birthday.
See also: Buckminster Fuller and the Twelfth of July.
“Never show half-finished work.” So said R. Buckminster Fuller in the March 1960 issue of Architectural Design. By the time the phrase “never show half-finished work” appeared in his book Critical Path (1981), “Universal Requirements Checklist” had been renamed “Comprehensively Anticipatory Design Science’s Universal Requirements for Realizing Omnihumanity Advantaging Local Environmental Controls, Which are Omniconsiderate of Both Cosmic Evolution Potentials and Terrestrial Ecological Integrities.”
The evolution of the simple “Universal Requirements Checklist” to “Comprehensively Anticipatory Design Science’s Universal Requirements… ” is representative of Fuller’s process. Fuller’s ideas grow more complex each time they are presented, sometimes obscuring the original idea. But if you can find your way to that central early idea, there is often something of great value.
Everything is equally connected to everything in Fuller’s writing. Fuller was unable to speak of mathematics, ethics, his individual life, global distribution of goods and services - everything - without speaking of all of it. You’d recognize it as the way crazy men talked, if crazy men were courted by publishers and universities all over the planet, and if crazy men earned dozens of ground-breaking patents, and most of all if crazy men and their crazy ideas didn’t turn out to be merely decades ahead of their time. I have some half-finished work by Fuller in which he clearly states an idea decades ahead of when he said it. I also have the finished work, still ahead of its time but nearly impenetrable in how it is presented.
The clearly stated work is a transcription of a recording Fuller made in the late 1960s. The transcriptions reside in Box 9, Folder 3 of the Stanford University Special Collection of R. Buckminster Fuller. The transcriptions document a series of discussions between Fuller and his patent attorney, D. Verner Smythe. The patent was not pursued and does not appear in Inventions, Fuller’s book of patents. The subject of the patent does, however, appear in Fuller’s magnum opus, Synergetics (1975 and 1979). To understand a node of Fuller’s thought requires tracing an idea across many other nodes of Fuller’s thought. But by tracing a line from diary entries through transcribed monologues through published books, Fuller is shown to predict atomic-scale computers nearly forty years before today’s discussion of graphine semi-conductor computers.
The nucleus of Fuller’s story is a simple diary entry from 1 February 1928: “after much philosophical thought while walking about worked out theory of spheres.” By 1939, in a letter intended for publication to Joe Bryant, the walking about had been expanded upon. Now there were thoughts of suicide and murder, a mugging that broke Fuller’s cheek bone (never otherwise confirmed), and a disembodied voice that told him: “You think truthfully. From now on, you need never await temporal attestation to your thoughts.” By the 1970s the story included Fuller floating in the air, surrounded by a sphere of light. Fuller’s story pulses, from an amateur consideration of geometry to a blessing from the hand of God and back again.
Fuller’s theory of spheres is a synthesis of established mathematics, personal insights and numerology. His theory of spheres is a thought experiment that can be reproduced with physical models. Imagine a single sphere floating in space. Add another to it, and a third so that all three are touching each other. Add another sphere that touch only the first two so that the center of each sphere is on a plane. Add a fifth and a sixth sphere, both touching the initial sphere and its neighbor, and the result is six spheres around one. Three more spheres can be nested in the six spaces above and below the plane such that they touch the initial sphere and two of their neighbors.

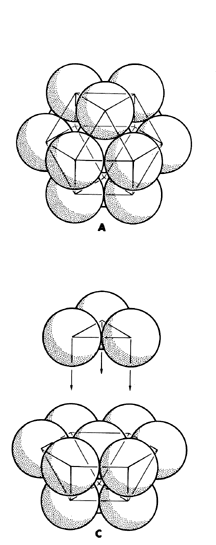
illustrations Copyright (c) 1975 the Estate of Buckminster Fuller.
IF three spheres nested below are staggered so that they alternately nest above and below the plane, the center of every sphere is an equal distance from all of its nearest neighbors, all spheres are an equal distance from the central sphere, and lines drawn from the center of all external spheres to their external neighbor form a cuboctahedron. A cuboctahedron is a polyhedron made up of eight triangular faces and six square faces. It can also be viewed as four interlocking hexagons, or a faceted globe with triangular poles and a hexagon equator.
Sphere-packing is an idea as old as the first stack of cannonballs or oranges. But Fuller’s theory of spheres led to a discovery that is unique. A tetrahedron made with ridged struts and flexible joints will hold its shape even when pressure is applied to a strut or a joint. Most other similarly constructed polyhedron will collapse under pressure. The cuboctahedron will also collapse, but in an interesting way. If pressure is applied to opposing triangular sets of struts, the hexagon between them will ripple. The struts double and form an octahedron (eight triangular faces). Between the cuboctahedron and octahedron, an implied icosahedron polyhedra (twenty sides) can be seen. And with a little hand work, the octahedron can be twisted into a triple-strutted tetrahedron. Fuller called this the “jitterbug transformation” and it is a mathematical insight that is his alone.
Having discovered the jitterbug transformation, Fuller considered it signficant and needed to find a use for it. He made a cuboctahedron cage of curved wire and rotated it on a globe until the wire least overlapped land masses. The cuboctahedron was the basis of his first Dymaxion Projection Map. The cuboctahedron was also the basis for Fuller’s earlier geodesic domes. In Fuller’s earlier geodesic domes a cuboctahedron was puffed up into a sphere, with the triangular and square faces faceted into smaller triangles and squares. Some of the lines that make up the faces run nearly all the way around such a sphere, and these Fuller called great circuits. The great circuits are the struts on Fuller’s earlier geodesic domes. Later he switched to “type two geodesic domes” based on the icosohedra, and an icosohedron based Dymaxion Projection Map. But he never abandoned his attraction to the cuboctahedron. He used it as a symbol for his mail order business in Philadelpha in the early 1980s.
Sphere packing (or as Fuller called it, the closest packing of spheres) twelve around one creates an implied cuboctahedron. If more spheres are placed around cuboctahedron, a larger cuboctahedron is formed. Every new layer of spheres makes a more sharply angled cuboctahedron, never a sphere. With one sphere in the center, the first layer has 12 spheres. The second layer will hold 42 spheres, the third layer 92, the fourth layer 162 and the fifth layer 252. All of these layers and every layer following ends in the number two. Round the number of spheres in a layer (10, 40, 90, 160, 250) and divide the numbers by ten and a progression by the second power is revealed (1, 4, 9, 16, 25). This is also an original discovery by Fuller.
The discovery could not be left as it was found. Fuller’s style of closest packing of spheres could not just be, it had to be meaningful. Adding the number of spheres in the first, second and third layer of spheres around a nucleus sphere (12 + 42 + 92) yields 146 spheres. This is the number of neutrons in the element uranium. Add 92 to 146 to yield 238, the number of neutrons and protons in the element uranium. From this numerological correspondence Fuller concluded that his style of sphere packing was descriptive of the structure of atoms, and thus all matter.
The cuboctahedron as a model for all matter, even this was not inclusive enough for Fuller. He imagined ideas were spheres. Not that spheres are a model for ideas, but that ideas were physical spheres. Some ideas are too specific to be of importance and some ideas are too general to be of importance. Ideas that are too specific are small spheres and ideas that are too general are large spheres. Small idea spheres will cluster around a center, large idea spheres will be pushed further from a central point. One idea is a free-floating nothing, two connected ideas might suggest something worth pursuing, three connected ideas point to a pattern, and four connected ideas form a tetrahedron. A tetrahedron of ideas will include ideas relevant to each thought and exclude irrelevant ideas, because a tetrahedron is the most simple polyhedron that has an inside and an outside (after spheres, I might add). Thus it takes four ideas to make a thought, and the shape of a thought is thus a tetrahedron. Fuller’s theory of spheres was a description of all matter and all consciousness.
These are examples of how Fuller’s thoughts breathed in and out, pulsed and jumped, danced a jitterbug. There was no clear demarkation line between established mathematics, numerology, personal biography, original insights, physical models and cosmic truths. There are good reasons to try and tease out what was original to Fuller and what he took from others, what is actionable and what is ornamentation. One of those good reasons is to speak plainly of when Fuller was decades ahead of his time, because sometimes Fuller was his own worst promoter.
In 1968 and 1969 Fuller met with his attourney Dale D. Klaus. The meeting was a monologue in which Fuller initiated a patent tentatively titled “Energy Systems for Computer Memory.” The trancribed meeting was combined with pages from the 1955 manuscript of what would later be published as Synergetics and Synergetics II. Fuller said his new kind of computer memory would differ from all existing computer memory:
Instead of having linear arrangements which is the way they tend to do things - linear and matrix array, I could do it omnidirectional phenomenon.
Fuller’s computer is a layered cuboctahedrons, each layer made of spheres. Fuller describes the spheres as glass coated with gold, silver, copper or aluminum depending on their location in the array. But Fuller also speaks of individual atoms of these materials, predicting by decades the nanocomputers under development today.
These layers of cuboctahedrons would have arrays of hexagons on their equators, and the nanocomputers of today are made of layers of hexagons. The fifth layer of a layered cuboctahedron of spheres would have the potential for a new nucleus sphere.
Conventional ciruits are described by Fuller as computing in a flat, ninety-degree, x/y array. Fulller’s computer would function in three dimensions at both sixty-degree and ninety-degree angles. The Fuller computer would begin a process with an electric impulse to the central, nucleus sphere. That signal would radiate out in all directions to the surrounding spheres. The radiating signal would terminate based on the strength of the signal, the material of the surrounding spheres, and the distance of a sphere from the nucleus sphere. The pattern of where the signal terminated constitutes stored information. Fuller speaks of his computer as made up of coated glass spheres, but also as single atoms of different elements.
I can lead a wire into one of the spheres at the center of the system and give that a load - and it would have to go out through it’s 12 contact points and by the frequency I give it I am sure I could round a special layer. […] I am planning to have a conductor to the center of the mass of atoms. There would be one atom that makes contact, we wouldn’t even have to see it. Well, the balls, the atoms by the time we get thorugh all the electrons actually have the same… we find with the electron microscope they look just like the same spheres. So by giving the right frequency and going out the right radial distance from there and pick up that information from millions and millions out there at that particular layer.
Three great circles could be done in gold, the four great circles could have been done in silver, the six great circles could have been done in copper and the twelve great circles could be done in aluminum. Now they are all conducting but they are all quite different.
Now about layers. If I were making this myself, say in ping-pong ball size, I couldn’t have very many layers. I figure in this room here I could have 100 layers or so. But if I were to use it… once I made this model then we would know this is exactly the same model as the closest packed spheres, as atoms. So then I would be able to assume millions of layers around a given atom.
Not all atoms but most atoms are packed that way […] So now we would be able for a given frequency… we would know how many special case informations we have stored there and how many relationships there are. […] There is no absolute continuum anyway so even those gold atoms… they happen to be closest and they will simply go from one to the other. But their resistances come in here, too. You will find there is a jump, there is a little jump from atom to atoms. A quantum jump.
There is a resistance difference due to the vertexes they go through. There is a resistance differential. Information can be stored in layer after layer and I think this is a storage system if you talk about compactness, there is nothing to compare it to.
I have re-arranged some of the above quotes to join like ideas, but I have not otherwise edited what Fuller said. His thinking-out-loud is not made up of complete and actionable ideas, but it does clearly point to an atom-sized hex-based system of computer memory. This is identical to the graphine memory systems now under development.
Compare the above rough take on Fuller’s computer with the following description as found in Synergetics:
I am confident that I have discovered and developed the conceptual insights governing the complete family of variables involved in realization by humanity of usable access to the ultimate computer… ultimate meaning here: the most comprehensive, incisive and swiftest possible information-storing, retrieving, and variably processing facility with the least possible physical involvement and the least possible investment of human initiative and cosmic energization. […] We have here the disclosure of a new phase of geometry employing the invisible circuitry of nature. The computer based on such a design could be no bigger than the subvisibly dimensioned domain of a pinhead’s glitter, with closures and pulsations which interconnect at the vector equilibrium stage and disconnect at the icosahedron stage in Milky-Way-like remoteness from one another of individual energy stars. […] The atomically furnished isotropic vector matrix can be described as an omnidirectional matrix of “lights,” as the four-dimensional counterpart of the two-dimensional light-bulb-matrix of the Broadway-and-Forty-second Street, New York City billboards with their fields of powerful little light bulbs at each vertex which are controlled remotely off-and-on in intensity as well as in color. Our four-dimensional, isotropic vector matrix will display all the atom “stars” concentrically matrixed around each isotropic vector equilibrium’s nuclear vertex. By “lighting” the atoms of which they consist, humans’ innermost guts could be illustrated and illuminated. Automatically turning on all the right lights at the right time, atomically constituted, center-of-being light, “you,” with all its organically arranged “body” of lights omnisurrounding “you,” could move through space in a multidimensional way just by synchronously activating the same number of lights in the same you-surrounding pattern, with all the four-dimensional optical effect (as with two-dimensional, planar movies), by successively activating each of the lights from one isotropic vector vertex to the next, with small, local “movement” variations of “you” accomplished by special local matrix sequence programmings. We could progressively and discretely activate each of the atoms of such a four-dimensional isotropic vector matrix to become “lights,” and could move a multidimensional control “form” through the isotropic multidimensional circuitry activating field. The control form could be a “sphere,” a “vector equilibrium,” or any other system including complex you-and-me, et al. This multidimensional scanning group of points can be programmed multidimensionally on a computer in such a manner that a concentric spherical cluster of four-dimensional “light” points can be progressively “turned on” to comprise a “substance” which seemingly moves from here to there. […] The ultra micro computer (UMC) employs step-up, step-down, transforming visible controls between the invisible circuitry of the atomic computer complex pinhead- size programmer and the popular outdoor, high-inthe-sky, “billboard” size, human readability.
The above quotes are from “Nuclear Computer Design,” section 427.00 of Synergetics. This is the same section in which Fuller suggest in antiquity humans were scanned atom by atom at a distant location and teleported to Earth by radio frequencies.
Teleportation aside, compare Fuller’s description of hexagon-based layered computer systems described in 1968 with these recent press releases…
- Multi-layer 3D graphene transistor breakthrough may replace silicon.
- New form of graphene allows electrons to behave like photons.
- All-graphene computer chip could steer us past the 22nm copper and silicon bottleneck.
- IBM builds graphene chip that’s 10,000 times faster, using standard CMOS processes.
It would sound like so much crazy talk, were he not also talking (in a byzantine way) of technologies the world is discovering to be true decades after Fuller described them.
SOURCES (Chronological)
Fuller, R. Buckminster: “Unviersal Requirements Check List.” Architectural Design March 1960.
Fuller, R. Buckminster: “Energy Systems for Computer Memory.” Unpublished manuscript 1968-1969.
Fuller, R. Buckminster: Synergetics. Macmillan Publishing Co. 1975.
Fuller, R. Buckminster: Synergetics II. Macmillan Publishing Co. 1979.
Fuller, R. Buckminster: Critical Path. New York: St. Martin’s Press 1981.
Lorance, Loretta: Becoming Bucky Fuller. Cambridge: MIT Press 2009.
Trevor Blake is the the author of The Buckminster Fuller Bibliography and The Lost Inventions of Buckminster Fuller.
Energetic-Synergetic Geometry 1962
R. Buckminster Fuller signed a book contract with Macmillan Publishing Company in 1961. The book in question, Synergetics, was not begun until 1969 and not published until 1975. The Energetic-Synegetic Geometry of R. Buckminster Fuller was published in a single, small-run edition in 1962 and has not seen print since. This is the first publication of the cover of this book, a small gift to the internet in honor of Fuller’s birthday. The twelfth of July was a special day for Fuller…
Buckminster Fuller Bibliography - Kindle Edition
Addendum 2016: See BOOKS for more information on Buckminster Fuller Bibliography and other books.
Fuller in Fashion
Fashion is design you wear, mobile and kinetic, including both tension and compression components. Fashion is the valve between the environment (everything except you) and the universe (everything including you). R. Buckminster Fuller’s influence on fashion is an undocumented parallel to his investigation into design.
☂ Fuller was attentive to his appearance. In Your Private Sky (Baden: Lars Muller Publishers 1999), Fuller is quoted as saying:
I decided to make a complete experiment of peeling off from society in general, and started wearing T-shirts which nobody was doing then, went about without a hat and in sneakers - absolutely comfortable clothes. Then when people started getting interested in my Dymaxion House, very nice people with influence, and they’d say, “l’d like to give a dinner party for you” and so forth, I would show up in khaki pants and they’d be very shocked. And when Mrs. John Alden Carpenter, head of the Arts Council in Chicago, gave a beautiful dinner party, I showed up and rudely announced, “I don’t eat that kind of food,” and was in every way obnoxious. l was putting self and comfort ahead of my Dymaxion House, and I said, “You’re not allowed to do that. You must get over that. You must stop that looking eccentric, with everybody pointing at this guy.” So I decided the way to do that was to become the invisible man, and that means a bank clerk - so I put on a black suit, bank clerk’s clothing; then they would focus on what I was saying instead of my eccentricities. I said, “I must get rid of continually making too much of myself.”
Fuller also knew of the attraction of the nude. When he exhibited the Dymaxion House in the 1920s, he placed a nude doll in its bedroom.
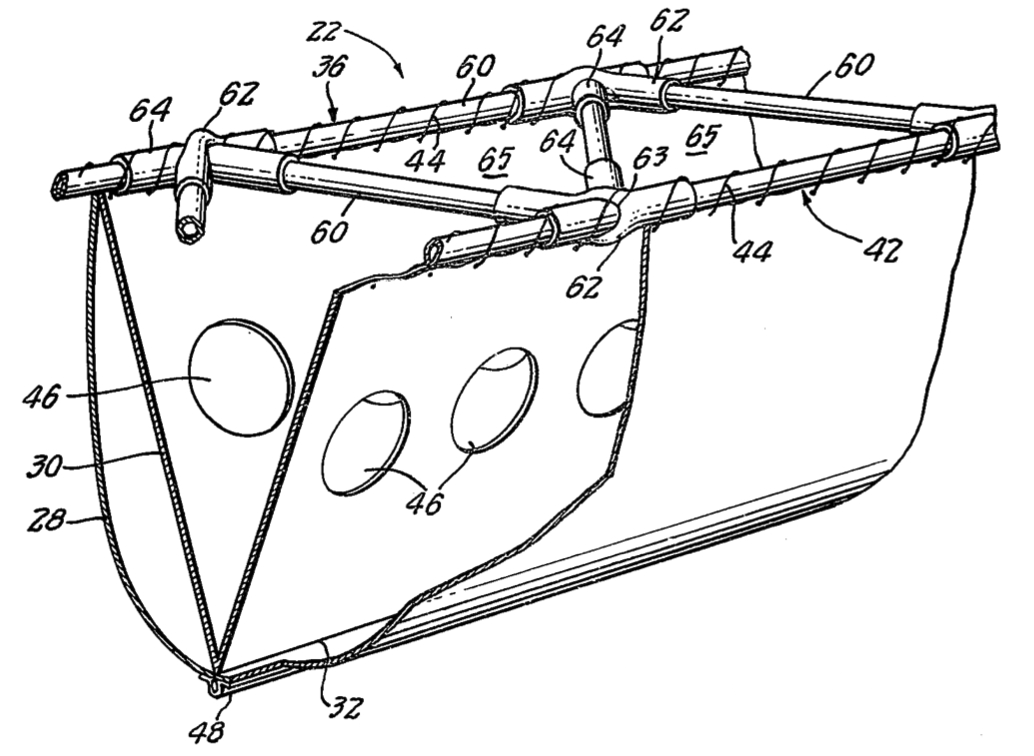
☂ Continuum Fashion is the source for this graphic showing one of a pair of irregular geodesic hemispheres…
The graphic is a glimpse into the mathematics of the N12, a bikini designed with a 3-D scanner and printed with a 3-D printer. Continuum writes:
The N12 bikini is the world’s first ready-to-wear, completely 3D-printed article of clothing. All of the pieces, closures included, are made directly by 3D printing and snap together without any sewing. N12 represents the beginning of what is possible for the near future. N12 is named for the material it’s made out of: Nylon 12. This solid nylon is created by the SLS 3D printing process. Shapeways calls this material “white, strong, and flexible”, because its strength allows it to bend without breaking when printed very thin. With a minimum wall thickness of .7 mm, it is possible to make working springs and almost thread-like connections. For a bikini, the nylon is beautifully functional because it is waterproof and remarkably comfortable when wet.
☂ “When I am working on a problem, I never think about beauty but when I have finished, if the solution is not beautiful, I know it is wrong.” This quote is attributed to R. Buckminster Fuller but I cannot find the source. More significantly, the greatest online biographer of Fuller - Joe S. Moore at his incredible buckminster.info - also cannot place this quote. Can you?
☂ Photographer Moria Simmons and a friend went as “Buckminster Fuller and the Geodesic Dame” on Halloween 2008. See Moria’s photograph here, and more of her photography (including a sneaky shot of the Dymaxion Car and the Fuller postage stamp) here. Could this be the same Moria who knitted a geodesic hat?
☂ Laura Dawson is a fashion designer. She used a geodesic dome to exhibit her Fall 2009 collection. (Thanks to grunch.net).
☂ The Buckminster Fuller Institute sells handbags and if memory serves they have sold pins and t-shirts in the past.
☂ Colleen Coghlan designed an inflatable type-two two-frequency geodesic pillow dome garment. She writes: “The inflatable dress (or ‘Wearable Space’) is, as the name describes, a garment that inflates into a personal space to sleep, rest or play within.”
Read more about the Wearable Space at The Cool Hunter.
☂ Connie Chang Chinchio sells a pattern for a geodesic cardigan.
☂ Life Magazine could have published a photograph of anyone assembling a Dymaxion Map in March 1943. They chose a contortionist in her circus uniform.
☂ Fuller Houses by Federico Neder (Baden: Lars Muller Publishers 2008) includes several items of Fuller fashion. The color plates section in the rear of the book shows a lapel pin of the Dymaxion House, presumably sold in the Henry Ford Museum where the Dymaxion House is on display. Fuller Houses also includes a sketch of a Dymaxion Hat designed by Irene Sharaff.
☂ The umbrella is a favored icon at synchronofile because it is a portable relatively inexpensive dome shelter produced on the industrial level. There are endless variations to the umbrella, from a banker’s basic black to the LED umbrellas of the film Blade Runner. The Bucky Bar was raised in February 2010. It was a geodesic dome made up of umbrellas designed by DUS Architects as a spontaneous (and unauthorized) dance bar in Rotterdam.
☂ Hair stylists Andreas and Markus contributed a two-frequency type two geodesic sphere hair weave to a fashion shoot by Purebred Productions.
☂ Florida-based Emilie produces beaded jewelry informed by energetic-synergetic mathematics.
☂ My first tattoo, which I gave myself around 1989, is a geometric shape referencing the work of Buckminster Fuller. No photographs of my tattoos have ever been published.
☂This essay first published on the twelfth of July 2011, a day of great significance to Buckminster Fuller.
- Trevor Blake
Trevor Blake is the author of the Buckminster Fuller Bibliography, available at synchronofile.com
R. Buckminster Fuller’s Influence on Science Fiction Films and Television

R. Buckminster Fuller’s influence on science fiction films and television during his lifetime (12 July 1895 – 1 July 1983).
First Spaceship on Venus
[Wikipedia] [IMDB] [youtube]
1960. Film. Directed by Kurt Maetzig. Based on the novel The Astronauts by Stanisław Lem. An international rocket crew finds geodesic domes on the planet Venus.
Earth II
[IMDB]
1971. Television. Directed by Tom Gries. A space station makes a claim for independence from the Earth it orbits. R. Buckminster Fuller is credited as the “Technical Advisor for Earth” in Earth II. Fuller’s Dymaxion Map is used to track orbiting satellites in an Earth-bound control room.
Slaughterhouse 5
[Wikipedia] [IMDB] [youtube]
1972. Film. Directed by George Roy Hill. Based on the novel Slaughterhouse Five by Kurt Vonnegut Jr. Billy Pilgrim is kept in a geodesic dome in a zoo on the planet Tralfamadore.
Silent Running
[Wikipedia] [IMDB] [youtube]
1972. Film. Directed by Douglas Trumbull. The spaceship Valley Forge includes several geodesic domes.
The Starlost
[Wikipedia] [IMDB] [youtube] [The Starlost: The Word]
22 September 1973 – 5 January 1974. Television. Directed by Leo Orenstein. Created by Harlan Ellison. Executive Producer was Douglas Trumbull of Silent Running. A geodesic dome from the spaceship Valley Forge from Silent Running is re-used on the spaceship The Ark.
Battlestar Galactica
[Wikipedia] [IMDB] [Battlestar Wiki: Agro Ship]
September 17, 1978 – April 29, 1979. Television. Created by Glen A. Larson.
The geodesic dome from the spaceship Valley Forge from Silent Running which had been re-used on the spaceship The Ark in The Starlost is re-used once more on an Argo Ship. This dome is on exhibit at the EMP Science Fiction Museum between 23 October 2010 - 4 March 2012.
See also LOST Domes.
- Trevor Blake
Trevor Blake is the author of the Buckminster Fuller Bibliography, available at synchronofile.com
Geodesic Domes and Earthquakes
Trevor Blake has not been compensated by any manufacturer found in this article. Always consult with a professional before the construction or purchase of any building.

U.S. Air Force C-17 Globemaster III airdrops humanitarian aid into the outskirts of Port-au-Prince, Haiti, 18 January 2010. Photograph by U.S. Air Force photo/Tech. Sgt. James L. Harper Jr. Source: wikipedia.
R. Buckminster Fuller made claims about how geodesic domes would weather an earthquake. In Perspecta Vol. 1 (Yale School of Architecture, Summer 1952) Fuller claims geodesic domes will arrive at “predictably stable conditions under extreme stress of earthquakes.” In Inventions (St. Martin’s Press, 1983) Fuller wrote:
When I invented and developed my first clear-span, all-weather geodesic dome, the two largest domes in the world were both in Rome and were each 150 feet in diameter. They are St. Peter’s, built around A.D. 1500, and the Pantheon built around A.D. 1. Each weighs approximately thirty thousand tons. In contrast, my first 150-foot-diameter geodesic all-weather dome installed in Hawaii weighs only thirty tons – one-thousandth the weight of its masonry counterpart. An earthquake will tumble both the Roman 150-footers, but would leave the geodesic unharmed.
On 12 January 2010 the island nation of Haiti experienced a 7.0 M earthquake. Thousands were killed, thousands more are now without shelter. If Haiti had more geodesic domes, would fewer have died and would fewer now be without shelter? Some testing of domes and their integrity during earthquakes has occurred since Fuller’s time.
Both professional and amateur dome builders have made claims about how geodesic domes can weather an earthquake. Timberline Domes writes: “Geodesic structures have shown themselves to endure through severe storms and earthquakes, due to the strength of their design.” Michael W. Johnson was introduced to the geodesic dome at the Design School at North Carolina State University. Fuller and some NCSU students had built domes as early as 1949. Mr. Johnson moved to El Salvadore in the 1970s, where in 1977 he experienced an earthquake. Since that time Mr. Johnson has penned an essay titled Geo Dome Homes for the Third World on building geodesic domes using local materials as a means of weathering earthquakes. These domes were scheduled to be built after July 2008. The Loma Prieta earthquake of 17 October 1989 was measured at a magnitude of 6.9. According to Oregon Dome Information Series #11, Disaster Fitness, this earthquake left the family of Joan Fevaros homeless. A few doors from the remains of their home was a still-standing geodesic dome home that offered them temporary shelter. “When [the Favaros family] went to the county building department to get a permit to demolish their old home to make way for a new one, they were told that the county would not allow any two-story homes to be built. Joan told them that they wanted to build a new two-story dome home on the site of their old home. The county official replied, ‘Oh, if it’s a dome home, then that will be OK.'” Disaster Fitness makes similar claims for a 6.2 M earthquake on 28 June 1992 near Yucca Valley, California.
Some professional dome manufacturers are willing to put their claims to the test, including direct aid to Haiti. American Ingenuity warranties their domes against structural damage due to hurricanes, earthquakes and tornadoes. From the A.I. Warranty:
Your dome home is designed to withstand the powerful forces of nature. American Ingenuity’s warranty or guarantee assures against any structural storm damage as a result of the ravages of tornadoes, earthquakes, hurricanes regardless of the force. Such a warranty has been unheard of in the construction industry until now. […] The founder of American Ingenuity, Michael Busick, manufactured and built his first concrete dome in 1976. Since then no American Ingenuity Dome has suffered any structural damage due to hurricanes, tornadoes or earthquakes.
Pacific Domes has made a one-time offer of up to 50% off list prices to send shelters to Haiti and will match donations made to World Shelters, World Shelters has its own international earthquake disaster relief effort involving geodesic structures and is supported by Humbolt State University class Engineering 305 Appropriate Technology. Monolithic Domes does not manufacture geodesic domes. Monolithic domes are manufactured by inflating a hemispherical shape then covering that shape with steel-reinforced concrete and insulation. What a Monolithic dome might lack in being mobile, it compensates for in being durable. Monolithic Domes were inspired by a 1950s lecture by Fuller. Monolithic Domes and musician Won-G had planned to build Monolithic domes in Haiti several weeks before the earthquake. This dome will house five hundred and is part of the One Dome at a Time project.
While before-the-fact claims about geodesic domes and earthquakes are easy to find, after-the-fact accounts of geodesic domes and earthquakes are difficult to find. The Materials Park Building of ASM International is housed under a geodesic dome raised in 1959. This dome was designed by William Hunt Eisenman, John Terence Kelly, and Fuller. It was manufactured by the North American Aviation Company. The ASM dome weathered a 5.0 M earthquake on 31 January 1986. The extent of the damage was the sheering of a few bolts. In this case, it appears Fuller’s claims about geodesic domes and earthquakes are accurate.
Geodesic domes may or may not have more integrity in an earthquake than other structures. They have not been tested enough to make further claims. But geodesic domes as emergency shelters are well tested and could be part of relief efforts in Haiti and elsewhere.
- Trevor Blake
Trevor Blake is the author of the Buckminster Fuller Bibliography, available at synchronofile.com.
LOST Domes
The television program LOST (first broadcast on the United States channel ABC between 2004-2010) includes geodesic domes. This essay will discuss the geodesic domes appearing in LOST without giving away the story.
The LOST dome has been seen in three forms. The first version of the dome is the dome itself, seen in the episode “Man of Science, Man of Faith” on 21 September 2005. This dome is a full-sized set, while the other two are models. It is implied that this dome is a 5/8th-sphere made up of panels an entryways. The second version of the dome is a model of the completed dome, seen in the episode “Orientation” on 5 October 2005. This dome is a cutaway model made of panels of a 5/8th-sphere. The second version of the dome is a model of the dome under construction, seen in the episode “Namaste” on 18 March 2009. This dome is an in-progress 5/8th-sphere made of struts. The “Man of Science” dome and another dome appear in the computer game LOST: Via Domus. All of the geodesic domes appearing in LOST are class one, four-frequency, 5/8ths truncated spheres.
The word geodesic is made up of the root words geo (Earth) and desic (divide). A geodesic sphere is a sphere divided by lines. The equator around the Earth is a geodesic line, dividing the Earth into a Northern and Southern hemisphere (partial sphere). The equator and the Prime Meridian line divide the Earth into four sections. A longitude line 90-degrees from the Equator and from the Prime Meridian would divide the Earth into eight sections. Were the points where these lines cross connected within the Earth, the connections would form an octahedron. If the triangular faces of that octagon are subdivided into smaller triangles each, and if these triangles are projected out from a central point onto the surface of the earth, it will form the coordinates for a geodesic sphere. Geodesic spheres can also be projected out from an imagined icosahedron inside a sphere. If the triangular faces of an icosahedron are subdivided into smaller triangles and these smaller triangles are projected out from a central point onto the surface of a sphere, the familiar pattern of a geodesic sphere is seen. Fuller initially referred to alternative and regularâ domes, but the terms class one and class two have become standardized terms.
Class one and class two domes are differentiated by how the faces of a polyhedron (in this case, the triangular faces of an icosahedron) are subdivided before being projected out from a central point onto the surface of a sphere . A class one dome divides the faces of a polygon more or less parallel to the edges of the polygon. A class two dome divides the faces of a polygon more or less perpendicular to the edges of the polygon. To see the difference, draw two triangles. Place a mark in the center of each edge of each triangle. On the first triangle, draw a line connecting the marks. On the second triangle, draw a line connecting the mark to the opposite angle. The first triangle will be subdivided into four smaller triangles, one in the center and one in each corner. The second triangle will be subdivided into six smaller right-angle triangles, each one touching a center point. The first triangle is how the face of an icosahedron is subdivided in a class one geodesic sphere. The second triangle is how the face of an icosahedron is subdivided in a class two geodesic sphere. The LOST domes are class one domes.
The frequency of a geodesic sphere is how many times a projected polygon face is subdivided. An icosahedron has a frequency of one (or 1v), as its faces are not subdivided. The first triangle mentioned in the previous paragraph, the subdivided triangular faces found in a class one geodesic sphere, are two frequency (or 2v). Triangular faces on an icosahedron can be divided into any number of frequencies. Low frequency geodesic spheres have the advantage of a uniformity of components. High frequency geodesic spheres have the advantage of a closer approximation to a sphere. Most of the triangles on a geodesic sphere can be seen as part of a hexagon. Some triangles, however, are also part of pentagons. The edges of the triangles making up pentagons on geodesic spheres radiate from a central point to another pentagon on the sphere. Counting the number of edges from pentagon to pentagon (including edges in a pentagon) reveals the frequency of a geodesic sphere. The LOST domes have a pentagon at the highest point.
The LOST domes are not geodesic spheres, but are instead geodesic domes. A single pentagon of five triangles on a 4 frequency geodesic sphere is a 1/8th truncated sphere. Adding the band of triangles around that pentagon makes a 1/4th truncated sphere. The LOST domes are 5/8ths truncated spheres. Geodesic spheres truncated into domes are a collision point between mathematical purity and architectural integrity. The truncation lines of a geodesic sphere are nearly flush with a surface to sit on, but not exactly flush. Readers are encouraged to join many generation of amateur geometric dome model builders. Desert Domes offers an online calculator for finding component measurements of a 4 frequency geodesic sphere and 1/2 truncated sphere.
The narrative of LOST places the construction of these geodesic domes in the mid-1970s. In the mid-1970s Buckminster Fuller was at the height of his popularity and influence. The use of domes in LOST helps establish when the story is taking place and the sympathies of the characters that constructed them.
References
‘Man of Science, Man of Faith’
lostpedia.com | hulu.com
‘Orientation’
lostpedia.com | hulu.com
‘Namaste’
lostpedia.com | hulu.com
Lost: Via Domus
lostpedia.com | ubisoft.com
- Trevor Blake
Trevor Blake is the author of the Buckminster Fuller Bibliography, available at synchronofile.com
Buckminster Fuller and the Homeless of New York
If Buckminster Fuller is known for any effort, it is the effort to provide shelter. But who did Fuller actually provide shelter for? The Lightful House and 4D House existed only on paper. The Dymaxion House existed only as a small scale model. The Dymaxion / Wichita House existed as two full-scale models (one internal, one external, neither able to be connected to the other). The Dymaxion Deployment Unit did house a small number of US armed forces personnel but the DDU was the invention of Victor C. Norquist, not Buckminster Fuller. The geodesic dome was invented by Walter Bauersfeld. Of the dozens of books by and about Fuller, of the thousands of articles on his life and work, most of them fail to give a single instance of when Fuller actually provided shelter to anyone. The Buckminster Fuller Bibliography by Trevor Blake is the first book to document that Fuller provided shelter for others with his own direct effort.
The New York Times for 10 September 1932 includes an uncredited article titled “Single Jobless Men to Get Lodging House / Social Worker and Engineer Obtain Use of Tenement for Those Ineligible for City Aid.” The building in question was a then-deserted seven-story building located at 145 Ridge Street in New York City, New York. The social worker was Ben Howe and the engineer was Buckminster Fuller. Fuller is described as “editor of the magazine Shelter and head of Structural Study Associates, an engineering firm.” According to the article, the men who were renovating the building were hoping to live in it afterward. They were otherwise ineligible for benefits because they were not the head of a family. The building was to house two hundred and fifty men at a time and serve several thousand during Winter. Lieutenant R. E. Johnson was also involved in this project. He is described as a “former army construction engineer and commander of the United States Ex-Service Men’s Association.” At the time of the article, the shelter was under construction. The building described in this article no longer exists.
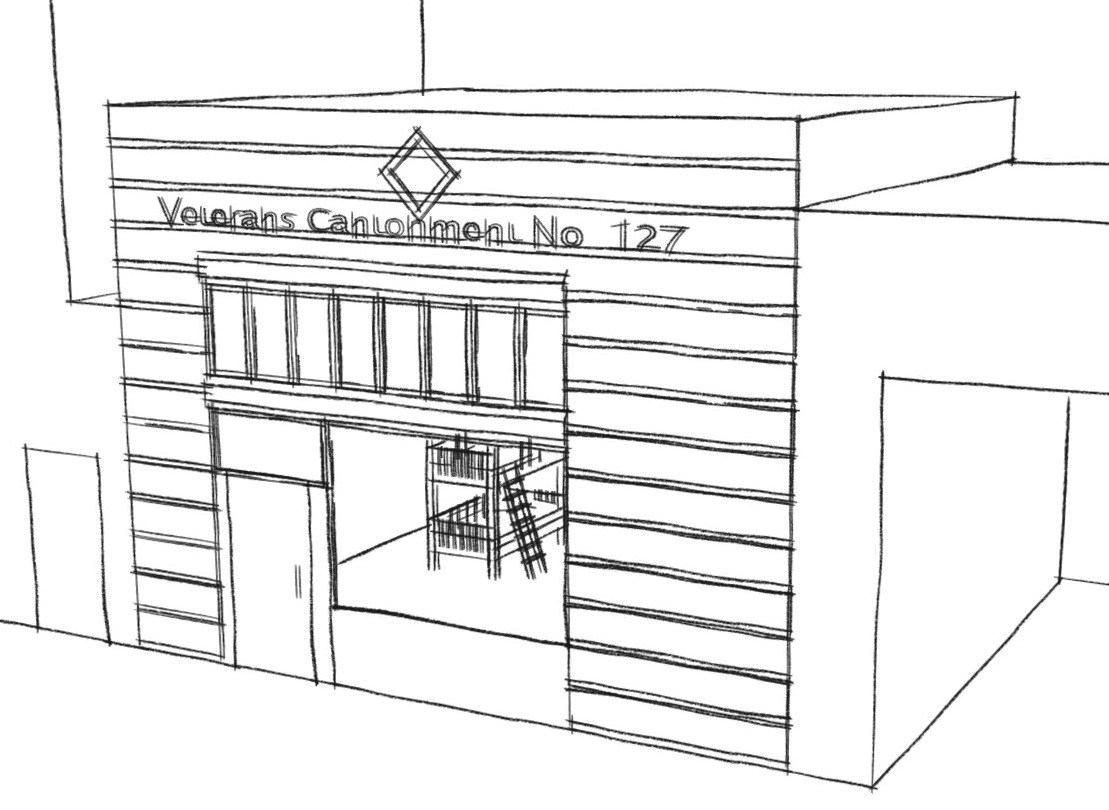
The New York Times for 2 December 1932 includes an uncredited article titled “Jobless Veterans Back in Barracks / 300 Single Men to Live Under Military Rule in Converted Clubhouse in 54th St.” The building in question was a five-story converted boy’s club at 340 East 54th Street in New York City, New York. According to the article, the shelter would be run by and for veterans and in a military style. The shelter would serve single men because of their difficulties in obtaining relief from existing services. The plan was initiated by a meeting of representatives of various interested organizations at the office of Raymond V. Ingersoll. Ingersoll served as a New York Parks Commissioner and as a Brooklyn Borough President. A residential development named after Ingersoll stands today at 120 Navy Walk in Brooklyn, New York. The representatives at the meeting included Ben Howe and Buckminster Fuller of the 145 Ridge Street shelter, Philip Hiss, Colonel Walter L. DeLamater, Arthur Huck, Louis Gleich, Owen R. Lovejoy, Cyrus C. Perry, James R. Sichel and Henry C. Wright. Philip Hiss went on to design and build homes in Florida, although he was not a trained architect. Col. DeLamater served in the 71st Infantry Regiment, an organization of the New York State Guard. Arthur Huck worked on numerous homeless shelter projects in the New York area, as reported in decades of articles found in the New York Times. Louis Gleich was a commander in the New York County Council of the Veterans of Foreign Wars and was the chairman of the committee that erected a VFW monument in Union Square. Owen Lovejoy served as the General Secretary of the National Child Labor Committee. The building formerly housed the Kips Bay Boys’ Club, where Lovejoy served as secretary. The building was to be called Veterans Cantonment No. 1. At the time of the article, the shelter was in operation. The building described in this article may still exist, next to the building that currently is designated as 340 East 54th Street.
By 1932, Buckminster Fuller had published drawings of his 4D House and exhibited models of his Dymaxion House. He had been featured in the Chicago Evening Post, Fortune Magazine, the Harvard Crimson, Modern Mechanics Magazine, the New York Times and Time Magazine. Fuller had published his monograph 4D and was publishing Shelter Magazine. He had earned the rank of Lieutenant Junior Grade in the United States Navy. In 1933 Fuller would begin work on the Dymaxion Car.
What makes these homeless veteran shelters distinct from any other that Fuller was involved with was that they provided actual shelter to actual men. While they do not have the glamor of Fuller’s Dymaxion House and other creations, they hold the advantage of having existed. Giving a new purpose to an existing structure was an idea that Fuller seldom developed but never abandoned. In his 1970 book I Seem to Be a Verb, Fuller wrote: “Our beds are empty two-thirds of the time. Our living rooms are empty seven-eights of the time. Our office buildings are empty one-half of the time. It’s time we gave this some thought.”
- Trevor Blake
Trevor Blake is the author of the Buckminster Fuller Bibliography, available at synchronofile.com
Reference:
71st Infantry Regiment (New York). 1 April 2009. Wikipedia. 22 May 2009. http://en.wikipedia.org/wiki/71st_Infantry_Regiment_(New_York)
Davis, Edwards: “Advocates the Standardizing of Industry by Law.” New York Times [New York City, New York] 27 July 1913: SM14
Fuller, R. Buckminster. I Seem to Be a Verb. New York: Bantam Books, 1970.
Ingersoll, Raymond V. Houses. 2009. New York City Housing Authority. 22 May 2009. http://www.nyc.gov/html/nycha/html/developments/bklyningersoll.shtml
“Louis Gleich, 69, Dies.” New York Times [New York City, New York] 26 Sept 1961: 39.
“Philip H. Hiss 3d, 78, Designer of Buildings.” New York Times [New York City, New York] 4 November 1988: B4.
Sieden, Lloyd S. Buckminster Fuller’s Universe. Cambridge: Perseus Publishing, 1989.
The Lost Inventions of Buckminster Fuller (Part 3 of 3)
The Lost Inventions of R. Buckminster Fuller is a three-part investigation into the inventions of Buckminster Fuller. These essays can serve as companion essays for two previous books by and about Fuller: Inventions (Fuller, St. Martin’s Press 1983) and The Dymaxion World of Buckminster Fuller (Marks and Fuller, Doubleday 1973). Ownership of these two books is not necessary for reading these essays. Page numbers without citations are from Inventions Fuller made many claims about his inventions, claims which are confirmed or called into question by these essays. A new appreciation for Fuller’s innovations is the result.
Fuller claimed that his life goal was to provide humanity with the means to save itself from itself and from natural disasters. To that end Fuller could have given his inventions up to the public domain, making them more accessible to more people. But Fuller sought, obtained and defended patents for many of his inventions, for two reasons.
First, Fuller hoped that the long-term and public nature of the US Patent Office would serve as a long-term and public record of his work. Fuller wrote in Inventions: “The public record established by my patents […] can serve as a critical appraisal of the historical relevance, practicality, and relative effectiveness of my half-century’s experimental commitment to discover what, if anything, an individual human being eschewing politics and money-making can do effectively on behalf of all humanity.”
Second, Fuller hoped to prevent others from profiting from his inventions. Donald W. Robertson served as Fuller’s patent attorney and wrote about his experience in The Mind’s Eye of Buckminster Fuller (Robertson, St. Martins 1983). Robertson described why Fuller sought patents: “While Fuller did not wish to seek patent profits by selling efforts, he was adamant in seeking to forestall efforts of others to profit by making unauthorized use of his inventions.” Fuller defended his patent interests. Fuller’s archive includes legal disputes over royalties with North American Aviation between 1958 and 1961 and with Ernest Okress between 1978 and 1979. According to Siobhan Roberts’ book on mathematician Donald Coxeter, King of Infinite Space (Roberts, Walker & Co. 2006), Fuller’s patent on the Radome was defended in Canada by the United States Department of Defense. Fuller sought and sometimes obtained intellectual property rights in Argentina, Belgium, Bolivia, Brazil, Canada, Chile, Columbia, The Congo, Costa Rica, El Salvador, Finland, France, Greece, India, Iran, Iraq, Israel, Italy, Jamaica, Japan, Jordan, Kenya, Korea, Luxembourg, Mexico, New Zealand, Nicaragua, Norway, Pakistan, Panama, Paraguay, Poland, Portugal, South Africa, Spain, Switzerland, Turkey, the United State, the United Kingdom, Uruguay, Venezuela and West Germany.
All of Fuller’s inventions are lost in some way. All of Fuller’s U. S. patents are lost in that they have expired. Some of Fuller’s patents expired in his lifetime. This is due to his being unable to afford a renewal, or his deciding to let a patent expire, or perhaps neglect. Many of Fuller’s patents lost their references to earlier patents by other inventors. That is, what Fuller claimed he invented was in fact invented by someone else. Sometimes Fuller was ignorant of prior work, such as the octet-trus constructions of Alexander Graham Bell. Sometimes Fuller stole ideas whole-cloth, such Kenneth Snelson’s sculptures re-branded as Fuller’s tensegrity. Some of Fuller’s patents are lost because they have yet to go into production, existing only as scale models. Perhaps now that Fuller’s patents have expired some of them can be tested against Fuller’s claims. Perhaps the fog gun could be tested in arid environments, for instance. Many of Fuller’s patents are lost to the curious because they are not always filed under their popular name. The patent for the geodesic dome is to be found under the title ‘Building Construction,’ which has likely caused some researchers difficulty in finding it. Some of Fuller’s patents are lost because they are under-documented. Automobile restoration firm Crosthwaite and Gardiner had access to nearly all the information ever produced about the Dymaxion Car, but at times had to make their best guess in the creation of Dymaxion Car #4 because detailed schematics and photographs were not available. The credits to many of the illustrations in Inventions are lost. Illustrations appear in the book without further information. The photograph on the front cover is a 36-foot geodesic dome made by students at the University of Minnesota and assembled in Aspen, Colorado in 1952. Additional photographs of this dome can be found in Dymaxion World illustrations 334-339. The end papers show the paperboard dome of 1954. Page vi shows Fuller with a partially-assembled model of the 4D House in New York City in 1929. Page xi shows Fuller at Black Mountain College in 1948. Pages xvii and xviii appear to be Fuller at the Montreal World’s Fair dome. The photographs on pages xiv, xxvi-xxvii, xxxi and xxxii are of unknown origin.
Tetrahedron City is a floating city proposed by Fuller in the early 1960s and described in Dymaxion World. Fuller never sought a patent for Tetrahedron City. Tetrahedron City is an equilateral tetrahedronal city two miles long at its base edge, housing one million people in three hundred thousand apartments. Each apartment would have an ocean front balcony. City infrastructure is located in the interior of the tetrahedron, airstrips are located along the base exterior. The foundation of Tetrahedron City is made up of hollow box-sectioned reinforced concrete, providing buoyancy. The size of the city provides stability even in ocean storms.
Tetrahedron City would be slightly more than 1.6 miles in height. This is three times the height of the Burj Khalifa in Dubai, United Arab Emirates, the tallest man-made habitat in history as of 2012 at 2,723 feet. Tetrahedron City would have an overall population comparable to Calgary, Canada and a population density comparable to Hong Kong, China. Tetrahedron City would be significantly more spacious and less populated than New York City, New York or Mexico City, Mexico. These cities have challenges but they cannot be said to be failures. The Robert Taylor Homes of Chicago, Illinois, however, were not able to meet their challenges. The Robert Taylor homes included two miles of housing spread among twenty-eight buildings, each sixteen stories in height. The Robert Taylor homes housed up to 27,000. In short order, these buildings became so rife with violence, poverty, arson and drug abuse that the only solution to these problems was to re-locate the residents and demolish the buildings. A similar outcome occurred in the Cabrini-Green buildings, also located in Chicago. The problems of these buildings were blamed both on gangs and a lack of green space or private space. How Tetrahedron City might address these problems remains to be determined.
Triton City is a floating city proposed by Fuller in the early 1960s and described in Dymaxion World. Fuller never sought a patent for Triton City. Triton City was designed to house up to five thousand people in one-fourth of a square mile, approximating the population of a small town under one roof. Triton City was to be a proof-of-concept module for the eventual creation of Tetrahedron City. The patron for Triton City was Matsutaro Shoriki. Shoriki is considered the father of Japanese professional baseball, and was the owner of newspapers and television stations. He was also considered the father of Japanese nuclear power, was under the pay of the Central Intelligence Agency to establish pro-USA television stations, and was a Class-A war criminal. Shoriki died after commissioning Fuller to design Tetrahedron City.
Fuller proposed the World Game in 1961 while lecturing at Southern Illinois University. The World Game was played on a large scale Dymaxion map representing Earth with students representing the population of the world. The goal of the game is to provide advanced access to goods and services to all people without resorting to war. The rules of the game are based on information on goods, services and transportation available to the World Game Institute. The information-gathering phase of the World Game echoes Fuller’s survey of industry from decades earlier. World Game has been played by students around the world to varying degrees of success. By the early 2000s the intellectual property of the World Game Institute had been purchased by O.S.Earth.

The Octet Truss is a building component made up of a tetrahedron and an octahedron with equal edge lengths. The Octet Truss is called Synergetic Building Construction in patent 2,986,241 (30 May 1961). Canadian patents were awarded in 1957. Grunch of Giants claims the Octet Truss was designed in 1933 and prototyped in 1949. Fuller claims that he owned a trademark, copyright and patent on the octet truss and that this was granted in part because he had shipped the structure across state lines. Shipping an invention across state lines is not a prerequisite for being granted a patent. In Genius At Work: Images of Alexander Graham Bell by Dorothy Harley Eber, Fuller claims to have been unaware of Bell’s octahedron-tetrahedron towers and kites. Bell was granted patent 856,838 for Connecting Device for the Frames of Aeriel Vehicles and Other Structures on 11 June 1907. This patent shows an modular octahedral-tetrahedral system “adaptable to a great variety of structural uses.” The octet truss is in use in the International Space Station, as Fuller claimed it would be. Closer to home, lighting rigs in theaters often use an octet-truss structure.
The Octet Truss is preceded by similar inventions, although there is no indication that Fuller was aware of them.
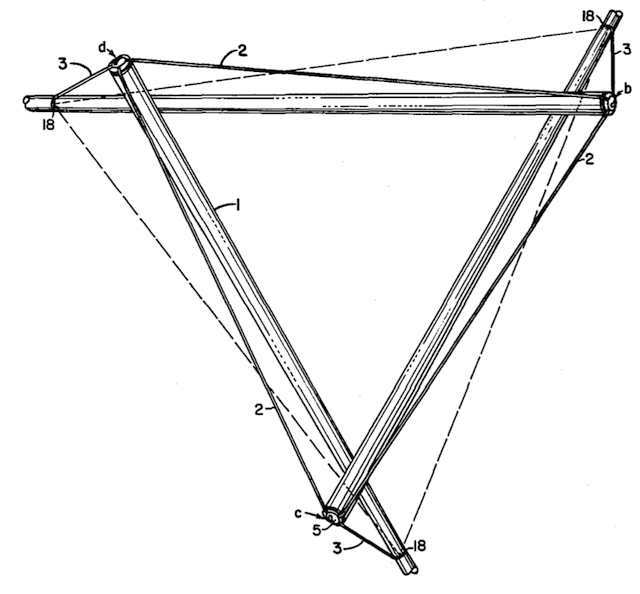
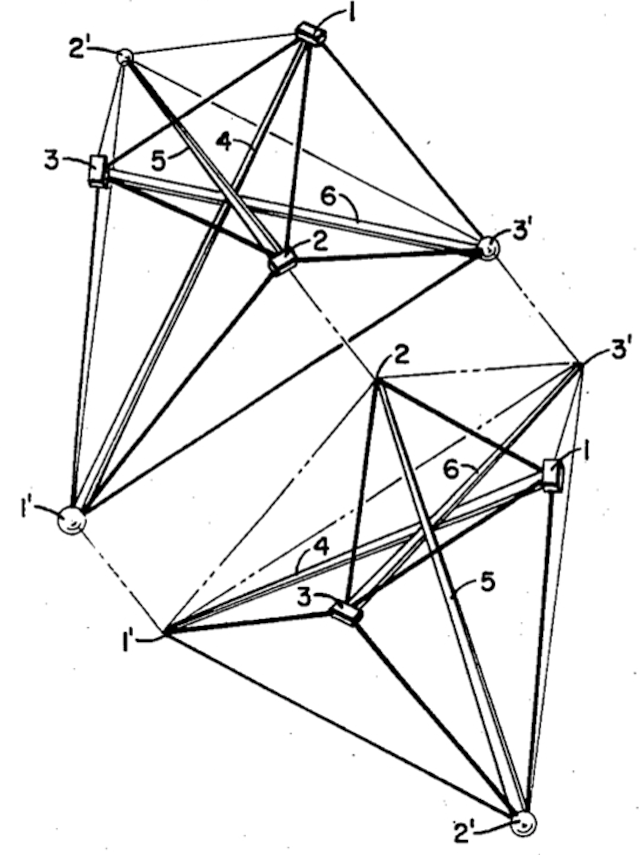
Tensegrity is a form of sculpture in which flexible wires are held taunt by struts, and the struts are held in place by the wires. Tensegrity is called Tensile-Integrity Structures in 3,063,521 (13 November 1962). Non-Symetrical Tensegrity is called Non-Symetrical Tension-Integrity Structures in 3,866,366 (18 February 1975). Canadian patents were awarded in 1960. Non-symetrical Tensegrity was patented in Canada, Great Britain, India, Italy and Japan in 1977. In Grunch of Giants, Fuller claims to have designed tensegrity in 1929. Buckminster Fuller invented the word tensegrity, but the structure described as a tensegrity was invented by Kenneth Snelson. The November 1990 issue of International Journal of Space Structures magazine includes a letter to the editors from Snelson on his sculptures and Fuller’s seizure of them.
When we got together again in June [1949] I brought with me the plywood X-Piece. When I showed [Fuller] the sculpture, it was clear from his reaction that he hadn’t understood it from the photos I had sent. He was quite struck with it, holding it in his hands, turning it over, studying it for a very long moment. He then asked if I might allow him to keep it. […] That original small sculpture disappeared from his apartment, so he told me at the end of the summer. [In] January 1951 he published a picture of the structure in Architectural Forum magazine and, surprisingly, I was not mentioned. When I posed the question some years later why he accredited me, as he said, in his public lectures and never in print, he replied, ‘Ken, old man, you can afford to remain anonymous for a while.‘
The two tensegrity patents in Inventions cite Dymaxion World, and illustration 265 in Dymaxion World mentions Snelson. The sculpture on page 179 was made by students at the University of Oregon in 1959. The sculpture on pages 184-185 was made by students at North Carolina State College in 1950. The sculpture on page 190 is claimed to have been exhibited at the Metropolitan Museum of Art in New York in 1959 but perhaps instead it was exhibited at the Museum of Modern Art in that same year, along with a geodesic dome and octet trus sculpture. At no time has a tensegrity been been as a shelter. Not for a home, a bridge, a garden shed, a bird house or any other sort of shelter. Tensegrities are fascinating sculptures but so far have no use in architecture.

Tensegrity is preceded by the sculptures of Kenneth Snelson, and Fuller was entirely aware of it.
The Geoscope was discussed in Fuller’s 1962 book Education Automation. The Geoscope was a proposed two-hundred-foot diameter sphere suspended by cables and covered in computer-controlled electric lights. Viewers outside or inside the Geoscope could see representations of migrations of people, goods and services on this miniature Earth. As with the Dymaxion Map, Fuller hoped that viewing the Earth as a whole would inspire whole-earth thinking rather than nationalist thinking.
Fuller never sought a patent for the Geoscope. It is preceded by the patent Exhibition Structure 655255 by Herbert P. W. Lyouns, awarded 7 August 1900. Exhibition Structure was a large globe covered in electric lights. Viewers outside or inside the Exhibition Structure could see representations of migrations of people, goods and services on this miniature Earth. Lyouns wrote: “The space within the globe will be divided by suitable partitions into rooms hallways and exhibition booths or apartments and an important feature of the invention is to locate these various rooms and apartments in such relation to the outlines on the outer surface of the globe as to permit the products of any particular country or city to be exhibited adjacent to the location of such country or city upon the map delineated upon the surf arc of the globe. Thus an important educational result is accomplished the visitor being enabled to associate in his mind the peculiar products of different countries with the geographical locations of such countries.”
The Geoscope is preceded by similar inventions, although there is no indication Fuller was aware of them.

The Submarisle (Undersea Island) is a buoyant underwater shelter anchored by cables to the sea floor. The Subgarisle is called an Undersea Island in patent 3,080,583 (12 March 1963). Jacques Cousteau’s Conshelf One housed two researchers for seven days in 1962, and Conshelf Two housed ten researchers for thirty days in 1963. The Submarisle is distinctive from Cousteau’s habitats in that it is buoyed on triangulated lines rather than resting on the sea floor. The Submarisle floats upward on three wires as Fuller’s Hanging Storage Shelf Unit hangs down from three wires.
The world has yet to see giant cargo submarines in need of submarisle docks. But drug runners are using very small submarines to transport their goods in the early 21st Century. Perhaps there are illegal and hidden submarisles in the world.
The Submarisle is the invention of Buckminster Fuller.
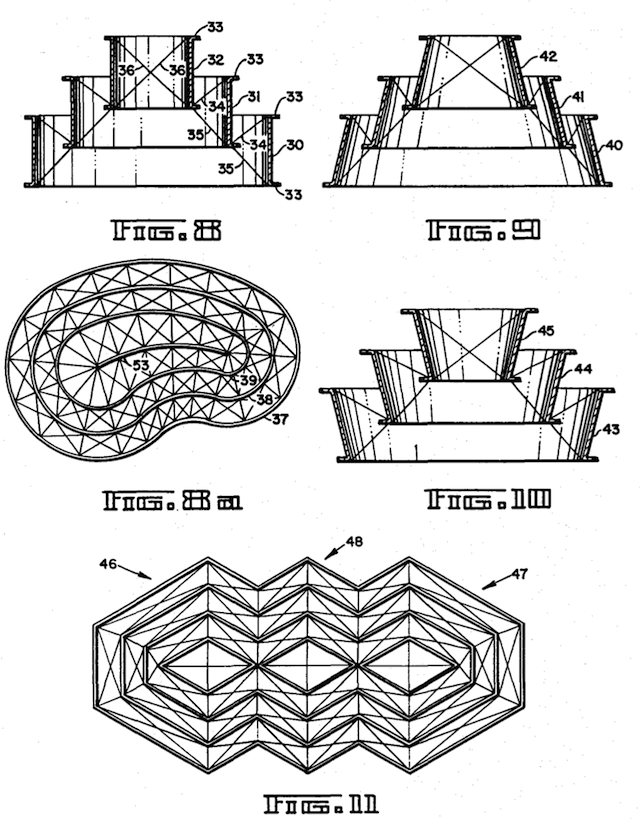
The Aspension (Suspension Building) is an architectural technique in which higher-up components are suspended by lower-down components. The Aspension Building is called a Suspension Building in patent 3,139,957 (7 July 1964). This is another invention by Fuller that has never been utilized commercially, although aspension structures exist as models.
The Aspension Suspension Building is a form of the sculptures of Kenneth Snelson, and Fuller was entirely aware of it.
The Octa Spinner (circa 1965) is a means of weaving tensegrity structures. The Octa Spinner has no patent. In Inventions, Fuller writes: “I did not go through with the octet spinner patent after filing because the expense of patent work is very great, and I’m not in the manufacturing world, and I felt that it would not be worth carrying any further.” The Mind’s Eye of Buckminster Fuller, however, claims that Fuller’s initial application was rejected and that he only ended the process after carrying it further into a second application. The Stockade patents are part of the manufacturing world, and much of his work on shelters could be considered the same. The Chronofile contains a folder labeled “Original Patents file: Octa Spinner (application withdrawn - case no. 349.021) March, 1965.”
The Star Tensegrity (Octahedral Truss) is a variety of tensegrity. The Star Tensegrity is called an Octahedral Building Truss in patent 3,354,591 (28 November 1967). Canadian patents were awarded in 1968. The photograph on page 248 shows the Union Carbide Tank Car Company Dome in Baton Rouge, LA USA. This dome was constructed in 1958 and demolished in 2007. The Octa-Hedronal Truss received a patent in Japan in 1965.
Tensegrity is preceded by the sculptures of Kenneth Snelson, and Fuller was entirely aware of it.

The Monohex (Geodesic Structures) is a variety of geodesic dome, made up of alternating hexagons and pentagons. The Monohex is called Geodesic Structures in patent 3,197,927 (3 August 1965). The photograph on pages 216-217 show the 50-foot Fly’s Eye dome built by John Warren. Additional photograph of this dome can be found on pages 210-211 of Buckyworks by J. Baldwin. The photographs on pages 222-223 are of unknown origin. The Monohex Geodesic Structure received a patent in Japan in 1979.
The Monohex Geodesic Structure, as a dome, is preceded by similar inventions. But the reduction of dome components to stackable interchangeable modules is a form unique to Fuller.

The Laminar Dome is a variety of geodesic dome, made up of alternating diamond shaped panels. The Laminar Dome is called a Laminar Geodesic Dome in patent 3,203,144 (31 August 1965). Canadian patents were awarded in 1961. The photograph on page 229 shows the same radome in illustration 415 of Dymaxion World, built by Western Electric.
The Laminar Dome, as a dome, is preceded by similar inventions. But the woven construction of this dome is a form unique to Fuller.
Energy Storage / Switching 1968-1969 is found in the Chronofile, housed at Stanford University. This is an invention in progress that is not otherwise documented.
Electronic Computer Energy Transformation 1969-1972 is found in the Chronofile, housed at Stanford University. This is an invention in progress that is not otherwise documented.

The Rowing Needles (Watercraft) is called a Watercraft in patent 3,524,422 (18 August 1970). Inventions does not give the filing date, which was 28 March 1968. In Dymaxion World illustration 298 this is called a minor invention of 1947. In Grunch of Giants, Fuller claims the rowing needles were invented in 1938 and prototyped in 1954.
Catamarans and outrigger canoes have existed since antiquity. As an avid sailor, Fuller would have been familiar with these crafts.
Cloud Nine is a floating city proposed by Fuller in Dymaxion World, published in 1973. Fuller never sought a patent for Cloud Nine. Fuller proposed that the air inside a one-mile-diameter geodesic sphere would weight more than the sphere itself. Sunlight would heat the surface of the sphere, heating the air inside, causing a temperature difference of the air inside and outside the sphere, and by this means the sphere would float upward. Fuller proposed many thousands of people could live in such a floating city, allowing it to drift or be guided.
The first manned hot air balloon (drifting) was demonstrated 1783 by the Montgolfier brothers. The first thermal airship (guided) was demonstrated in 1973, the year Dymaxion World was published. Stories of a city in the sky are found in antiquity. The Cloud Nine geodesic sphere, as a geodesic sphere, is preceded by similar inventions. But Buckminster Fuller’s Cloud Nine is an original proposal for how a floating city might be made.
Tiago Barros made a similar proposal nearly forty years later with his Passing Cloud.
The Passing Cloud is an innovative and environmentally friendly method of transportation that doesn’t require expensive steel tracks or concrete highways. It is made of a series of spherical balloons that form the shape of a cloud. Its inner stainless steel structure is covered with heavy weight tensile nylon fabric. During the journey, It moves according to prevailing winds speed and direction at the time of travel. Since it moves with the wind, no wind is ever felt during the trip, offering the passengers a full ‘floating sensation.’
Metabolics Money 7/11/1973 is found in the Chronofile, housed at Stanford University. This is an invention in progress that is not otherwise documented.

The Geodesic Hexa-Pent is called a Geodesic Pentagon and Hexagon Structure in patent 3,810,336 (14 May 1974). The patent was granted to Shoji Sadao and assigned to Fuller & Sadao, Inc. The Hex-Pent Dome was patented in Australia, Canada, India, Israel and Italy in 1973. Shoji Sadao was a former student of Fullers. Sadao was involved in the creation of the icosohedral Dymaxion Map (known as the Raleigh projection) and in the creation of the Expo ’67 dome in Montreal. In Inventions, Fuller claims that the Hexa-Pent dome was developed by Sadao and jointly named by Sadao and Fuller. The Hexa-Pent dome is preceded by patent 3,114,176 of Alvin E. Miller (17 December 1963).
The Geodesic Hexa-Pent dome, as a dome, is preceded by similar inventions. This patent was never claimed by Fuller. The Hexa-Pent dome was featured in the May 1972 issue of Popular Science magazine. The plans for the dome advertised on page 139 of this issue represents the only time Fuller himself sold dome instructions to the general public.
Helicopter Rotor Sail 1976 is found in the Chronofile, housed at Stanford University. This is an invention in progress that is not otherwise documented.
Fuller’s name for his thoughts was synergetics. Synergetics is a system of mathematics, an ethical system, a philosophy, an aesthetic, a form of poetry and more. Synergetics is the central invention of Fuller, with all the individual artifacts only special cases of synergetics. Hugh Kenner wrote that synergetics puts Fuller in the transcendentalist school, with his ancestor Margret Fuller. Elements of synergetics appear in Fuller’s earliest lectures and writing, but the 1975 publication of Synergetics can be considered a first full statement of his intent.
Fuller discovered a formula for predicting the number of spheres found in the outer shell of closest-packed spheres. That formula is ten times f squared plus two, with f equal to the frequency (number of layers). One sphere can be most closely surrounded by twelve identical spheres; six around the first sphere’s equator, three nestled underneath and three nested on top. This comprises the first layer, thus ten times one square plus two equals twelve, the number of spheres surrounding the original sphere. A second layer will have 43 spheres, a third will have 92 spheres, and so on. Fuller’s formula can predict the number of spheres on the outer shell of any array of closest-packed spheres.
Fuller formalized his Primitive Hierarchy of shapes in Synergetics 988.20 (1975, 1979). Fuller began with the claim thoughts are made up of ideas and that these ideas are spherical in shape. One idea is insufficient to form a thought, as would be two. Three ideas are close to a thought, but the connection between them has surface but no volume. Four spherical ideas packed together form a tetrahedron, a shape that has volume. Thoughts, therefore, are shaped like tetrahedrons. Fuller claimed that for this reason tetrahedrons were primal shapes and a more worthy basis for mathematics than cubes, grids or other systems.
If the volume of a tetrahedron is equal to one, then other shapes can be assigned volume in relation to the tetrahedron. The next larger shape in the Primitive Hierarchy is the cube. The volume of a cube is obtained by using the dual of the tetrahedron. To obtain a dual of a shape, make new edges at right angles to the center of the edge of a shape. The duel of a tetrahedron is another tetrahedron. The vertices of a tetrahedron and its duel form a cube. That cube will have a volume of three. The duel of that cube will form an octahedron with a volume of four. The duel of that octahedron will form a rhombic dodecahedron with a volume of six. These four shapes are a sufficient introduction to the Primitive Hierarchy, although Fuller identified larger and smaller shapes in the series.
Johannes Kepler proposed a different concentric hierarchy of shapes in his 1596 book Mysterium Cosmographicum. Kepler used the platonic solid shapes, and arranged them from (smallest to largest) as octahedron, icosahedron, dodecahedron, tetrahedron and cube. The idea of arranging shapes within other shapes is an ancient one. The Primitive Hierarchy is preceded by similar inventions. The Primitive Hierarchy is unique to Fuller.
The Floating Breakwater is patent 4,136,994 (4 February 1975) and the Floatable Breakwater is patent 3,863,455 (30 January 1979). These are breakwaters that float on the surface of the ocean to control the movement of the water or contaminants in the water. Fuller claims that he produced Floatable Breakwaters but there are no photographs of them in Inventions. Inventions does not give the filing date for either of these patents, which were 10 December 1973 and 19 September 1977 respectively. Dozens of floating breakwater patents, some generating power like Fuller’s Floatable Breakwater, predate Fuller’s patents. Lancelot Kirkup was granted patent 226,663 for his breakwater “loaded so to float that its greatest diameter will be about at the water line” on 20 April 1880.
The Floating Breakwater and Floatable Breakwater are preceded by similar inventions, although there is no indication that Fuller was aware of them.
The Tensegrity Trus is a variety of tensegrity. The Tensegrity Trus is called a Tensegrity Module Structure and Method of Interconnecting the Modules in patent 4,207,715 (17 June 1980). The patent was granted to Christopher J. Kitrick. Fuller wrote in Inventions: “I authorized Chris to take out a patent on his invention, which by agreement I paid for and on the basis it be assigned to me.” Fuller is not listed as assignee in this patent.
Tensegrity is preceded by the sculptures of Kenneth Snelson, and Fuller was entirely aware of it.
De-Resonated Tensegrity Dome 1981 is found in the Chronofile, housed at Stanford University. This is an invention in progress that is not otherwise documented.
Methods and Apparatus for Constructing Spheres 7/1/1982 is found in the Chronofile, housed at Stanford University. This is an invention in progress that is not otherwise documented.
The Hanging Storage Shelf Unit is a shelf suspended from the ceiling. The Hanging Storage Shelf Unit is patent 4,377,114 (22 March 1983). Inventions does not give the filing date, which was 5 October 1981. Fuller claims the hanging storage shelf unit was built and used in a bookstore, perhaps the unit shown in the photograph on page 295. The book on the shelf in that photograph is Dymaxion World thus the photograph could have been taken no earlier than 1973. The hanging storage shelf unit is not unlike the 1944 criss-cross tensionally supported table found in illustration 300 in Dymaxion World.
Patent 1,5952,466 (27 March 1934) was awarded to Alexander Sjodin, Charles J. Olund and Robert J. Moody. This patent is cited in Fuller’s patent for the Hanging Storage Shelf Unit. This Display Rack was suspended from above. Theodore Pollard was awarded patent 3,866,364 (18 February 1975) for Modular Structure for Use in Merchandising Operations. This consists of a hexagonal shelf that can be hung by wires.
The Hanging Storage Shelf Unit is preceded by similar inventions, and Fuller was aware of at least one of them.
Conclusion
R. Buckminster Fuller described himself as a “terrific package of experiences.” The record of Fuller’s uncredited duplication of prior work suggests that he was at times a terrific package of other people’s experiences. The greatest invention of Richard Buckminster Fuller was the character Bucky.
- Trevor Blake
Trevor Blake is the author of the Buckminster Fuller Bibliography, available at synchronofile.com



